Fourier-Transformation
Die Fourier-Transformation ist eine mathematische Funktion, die verwendet werden kann, um die Grundfrequenzen zu finden, aus denen ein Signal oder eine Welle besteht. Wenn zum Beispiel ein Akkord gespielt wird, kann die Schallwelle des Akkords in eine Fourier-Transformation eingespeist werden, um die Noten zu finden, aus denen der Akkord besteht. Die Ausgabe einer Fourier-Transformation wird manchmal als Frequenzspektrum oder -verteilung bezeichnet, weil sie ein Spektrum der Frequenzen der Eingabe anzeigt. Diese Funktion wird in der Kryptographie, Ozeanographie, beim maschinellen Lernen, in der Radiologie, in der Quantenphysik sowie beim Sounddesign und bei der Visualisierung vielfältig eingesetzt.
Die Fourier-Transformation einer Funktion f ( x ) {\darstellungsstil f(x)}
ist gegeben durch
F ( α ) = ∫ - ∞ + ∞ f ( x ) e - 2 π i α x d x {\Darstellung F(\alpha )=\int _{-\infty }^{{+\infty }f(x)e^{-2\pi i\alpha x}dx} 
α {\displaystyle \alpha } 
ist eine Frequenz
F ( α ) {\displaystyle F(\alpha )} 
ist die Fourier-Transformationsfunktion und gibt einen Wert zurück, der angibt, wie häufig die Frequenz α {\displaystyle \alpha } im ursprünglichen Signal vorkommt.
e - 2 π i α x {\displaystyle e^{-2\pi i\alpha x}} 
Stellt das Wickeln der Eingabefunktion f ( x ) {\darstellungsstil f(x)} um den Ursprung in der komplexen Ebene mit einer bestimmten Frequenz dar α {\darstellungsstil \alpha }
Die inverse Fourier-Transformation ist gegeben durch
f ( x ) = ∫ - ∞ + ∞ F ( α ) e + 2 π i x α d α {\d α {\displaystyle f(x)=\int _{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }d\alpha } 
Eine Fourier-Transformation zeigt, welche Frequenzen in einem Signal enthalten sind. Nehmen wir zum Beispiel eine Schallwelle, die drei verschiedene Musiknoten enthält: A, B und C. Wenn Sie die Fourier-Transformation dieser Schallwelle grafisch darstellen (mit der Frequenz auf der x-Achse und der Intensität auf der y-Achse), wird eine Spitze bei jeder Frequenz angezeigt, die einer der Musiknoten entspricht.
Viele Signale können durch Addition von Kosinus und Sinus mit unterschiedlichen Amplituden und Frequenzen erzeugt werden. Mit der Fourier-Transformation werden die Amplituden und Phasen dieser Kosinus- und Sinuswerte gegen ihre jeweiligen Frequenzen aufgetragen.
Fourier-Transformationen sind wichtig, weil viele Signale sinnvoller sind, wenn ihre Frequenzen getrennt werden. Im obigen Audio-Beispiel macht eine Betrachtung des Signals in Bezug auf die Zeit nicht deutlich, dass die Noten A, B und C im Signal enthalten sind. Viele Systeme machen unterschiedliche Dinge mit verschiedenen Frequenzen, so dass diese Art von Systemen dadurch beschrieben werden kann, was sie mit jeder Frequenz machen. Ein Beispiel dafür ist ein Filter, der hohe Frequenzen blockiert.
Die Berechnung einer Fourier-Transformation erfordert das Verständnis von Integration und imaginären Zahlen. Computer werden normalerweise zur Berechnung von Fourier-Transformationen von allem außer den einfachsten Signalen verwendet. Die schnelle Fourier-Transformation ist eine Methode, mit der Computer schnell eine Fourier-Transformation berechnen können.
· 
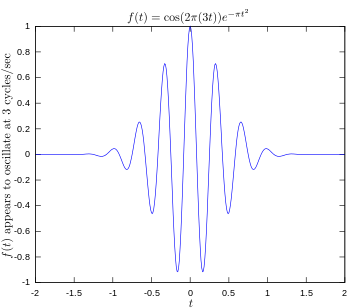
Originalfunktion, die ein mit 3 Hertz schwingendes Signal zeigt.
· 
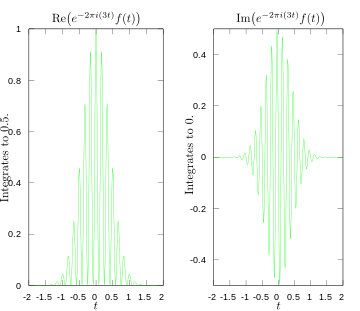
Real- und Imaginärteil des Integranden für die Fourier-Transformation bei 3 Hertz
· 
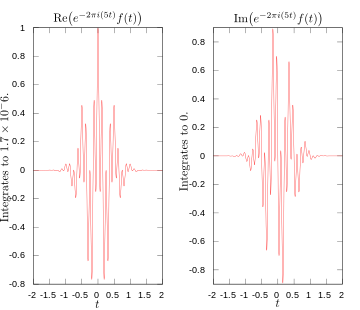
Real- und Imaginärteil des Integranden für die Fourier-Transformation bei 5 Hertz
· 
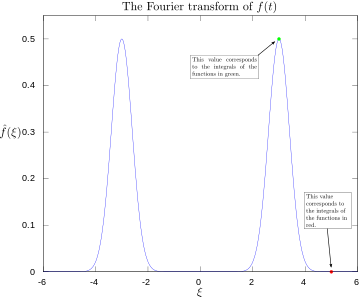
Fourier-Transformation mit 3 und 5 Hertz beschriftet.
Fragen und Antworten
F: Was ist die Fourier-Transformation?
A: Die Fourier-Transformation ist eine mathematische Funktion, mit der man die Grundfrequenzen einer Welle ermitteln kann. Sie nimmt eine komplexe Welle und findet die Frequenzen, aus denen sie sich zusammensetzt, so dass sie die Noten identifizieren kann, aus denen ein Akkord besteht.
F: Wie wird die Fourier-Transformation verwendet?
A: Die Fourier-Transformation wird in der Kryptographie, Ozeanographie, beim maschinellen Lernen, in der Radiologie, der Quantenphysik sowie beim Sounddesign und der Visualisierung eingesetzt.
F: Wie wird die Fourier-Transformation berechnet?
A: Die Fourier-Transformation einer Funktion f(x) ist gegeben durch F(ב) = ∫-∞+∞f(x)e-2נiבxdx wobei ב eine Frequenz ist. Dies gibt einen Wert zurück, der angibt, wie häufig die Frequenz ב im Originalsignal vorkommt. Die inverse Fourier-Transformation ist gegeben durch f(x) = ∫-∞+∞F(ב)e+2נixבdב.
F: Wie sieht eine Ausgabe einer Fourier-Transformation aus?
A: Die Ausgabe einer Fourier-Transformation kann entweder als Frequenzspektrum oder als Verteilung bezeichnet werden, da sie eine Verteilung der möglichen Frequenzen der Eingabe anzeigt.
Q: Wie berechnen Computer Fast Fourier-Transformationen?
A: Computer verwenden einen Algorithmus, der Fast Fourier Transform (FFT) genannt wird, um schnell alle Transformationen außer den einfachsten Signalen zu berechnen.
F: Was zeigt uns die Betrachtung von Signalen in Bezug auf die Zeit nicht?
A: Die Betrachtung von Signalen in Bezug auf die Zeit lässt nicht erkennen, welche Töne in ihnen enthalten sind. Viele Signale ergeben mehr Sinn, wenn ihre Frequenzen getrennt und stattdessen einzeln analysiert werden.
