Keplersche Gesetze
Die Keplerschen Gesetze der Planetenbewegung sind drei Gesetze, die die Bewegung der Planeten um die Sonne beschreiben:
- Planeten bewegen sich in elliptischen Bahnen um die Sonne. Die Sonne befindet sich in einem der beiden Brennpunkte der Umlaufbahn.
- Ein Liniensegment, das einen Planeten und die Sonne verbindet, fegt in gleichen Zeitintervallen gleiche Flächen aus.
- Das Quadrat der Bahnperiode eines Planeten ist proportional zum Würfel der Semihauptachse seiner Umlaufbahn.
Johannes Kepler fand diese Gesetze zwischen 1609 und 1619.
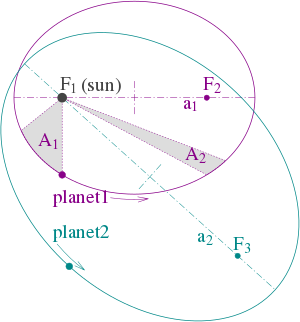
Abbildung 1: Illustration der drei Keplerschen Gesetze mit zwei Planetenbahnen. (1) Die Bahnen sind Ellipsen, mit den Schwerpunkten ƒ1 und ƒ2 für den ersten Planeten und ƒ1 und ƒ3 für den zweiten Planeten. Die Sonne befindet sich im Brennpunkt ƒ1. (2) Die beiden schattierten Sektoren A1 und A2 haben die gleiche Oberfläche, und die Zeit, die der Planet 1 benötigt, um das Segment A1 abzudecken, ist gleich der Zeit, die er benötigt, um das Segment A2 abzudecken. (3) Die Gesamtumlaufzeiten für Planet 1 und Planet 2 stehen im Verhältnis a13/2 : a23/2.
Vergleich mit Kopernikus
Die Keplerschen Gesetze verbessern das Modell von Kopernikus. Wenn die Exzentrizitäten der Planetenbahnen als Null angenommen werden, dann stimmt Kepler Kopernikus grundsätzlich zu:
- Die Umlaufbahn des Planeten ist ein Kreis
- Die Sonne im Zentrum der Umlaufbahn
- Die Geschwindigkeit des Planeten in der Umlaufbahn ist konstant
Die Exzentrizitäten der Bahnen der Planeten, die Kopernikus und Kepler bekannt sind, sind klein, so dass die obigen Regeln gute Annäherungen an die Planetenbewegung liefern; aber die Keplerschen Gesetze passen besser zu den Beobachtungen als die von Kopernikus.
Keplers Korrekturen sind keineswegs offensichtlich:
- Die Umlaufbahn des Planeten ist kein Kreis, sondern eine Ellipse.
- Die Sonne steht nicht im Zentrum, sondern in einem Brennpunkt der elliptischen Umlaufbahn.
- Weder die lineare Geschwindigkeit noch die Winkelgeschwindigkeit des Planeten auf der Umlaufbahn ist konstant, aber die Flächengeschwindigkeit ist konstant.
Durch die Exzentrizität der Erdumlaufbahn ist die Zeit von der März-Tagundnachtgleiche bis zur September-Tagundnachtgleiche, etwa 186 Tage, ungleich der Zeit von der September-Tagundnachtgleiche bis zur März-Tagundnachtgleiche, etwa 179 Tage. Ein Durchmesser würde die Umlaufbahn in gleiche Teile schneiden, aber die Ebene durch die Sonne parallel zum Äquator der Erde schneidet die Umlaufbahn in zwei Teile mit Flächen in einem Verhältnis von 186 zu 179, so dass die Exzentrizität der Erdumlaufbahn etwa
ε ≈ ≈ π π 4 186 - 179 186 + 179 ≈ 0.015 , {\displaystyle \varepsilon \approx {\frac {\pi }{4}}{\frac {186-179}{186+179}}}\approx 0.015,}
der nahe am richtigen Wert (0,016710219) liegt (siehe Erdumlaufbahn). Die Berechnung ist korrekt, wenn das Perihel, das Datum, an dem die Erde der Sonne am nächsten ist, auf eine Sonnenwende fällt. Das aktuelle Perihel, nahe dem 4. Januar, ist ziemlich nahe an der Sonnenwende vom 21. Dezember
Suche in der Enzyklopädie
