Weltlinie
Eine Weltlinie ist der einzigartige Weg, den ein Objekt auf seiner Reise durch Raum und Zeit, gewöhnlich Raumzeit genannt, zurücklegt. Wie wir aus der Speziellen Relativitätstheorie lernen, verlangsamt sich die Zeit für ein Objekt umso mehr, je schneller es sich bewegt. Wie Sie in der Abbildung rechts sehen können, hat das langsamere Objekt einen schnelleren Zeitverlauf als das sehr schnelle Objekt, für das die Zeit viel langsamer vergeht. Wenn ein Objekt die Lichtgeschwindigkeit erreicht, wird es auf der t-Achse null sein, was bedeutet, dass es in der Zeitrichtung keinen Fortschritt gemacht hat. Im Grunde zeigen die Weltlinien, dass bei Erreichen der Lichtgeschwindigkeit die Zeit für den Beobachter stehen bleibt. Weltlinien werden sehr oft in der theoretischen Physik und in der Speziellen Relativitätstheorie sowie in der Allgemeinen Relativitätstheorie verwendet.
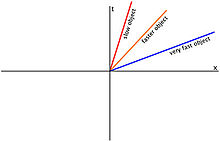
Die verschiedenen Bahnen von drei Objekten, die sich mit unterschiedlichen Geschwindigkeiten bewegen, und ihre jeweiligen Messungen des Zeitablaufs, wobei die t-Achse den Zeitablauf und die x-Achse die Geschwindigkeit des Objekts darstellt.
Verwendung
Das Konzept der Weltlinien ist in der theoretischen Physik weit verbreitet, denn es zeigt einige interessante Fakten über Hochgeschwindigkeitsbewegungen. Zum Beispiel ist die von Albert Einstein vorgestellte Zeitdilatationsgleichung algebraisch undefiniert, wenn die Geschwindigkeit eines Objekts die Lichtgeschwindigkeit ist, aber mit Weltlinien kann man feststellen, dass die Zeit stehen bleibt, wenn die Geschwindigkeit die Lichtgeschwindigkeit ist. Obwohl die Einsteinsche Gleichung (für die Zeitdilatation) zeigt, dass ein Objekt, das sich schneller als Licht bewegt, in der Zeit rückwärts läuft, kann dasselbe Konzept mit Weltlinien beschrieben werden.
| Teil einer Serie von Artikeln über | ||||||
| Allgemeine Relativitätstheorie | ||||||
|
G μ ν + Λ g μ ν = 8 π G c 4 T μ ν {\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }={8\pi G \over c^{4}}}T_{\mu \nu }} | ||||||
| ·
·
| ||||||
| Grundlegende Konzepte
| ||||||
| Phänomene
| ||||||
| ||||||
| Lösungen
| ||||||
| · v · t · e |
Fragen und Antworten
F: Was ist eine Weltlinie?
A: Eine Weltlinie ist der eindeutige Weg, den ein Objekt auf seiner Reise durch Raum und Zeit nimmt, normalerweise Raumzeit genannt.
F: Wie erklärt die spezielle Relativitätstheorie, wie die Zeit für Objekte vergeht, die sich mit unterschiedlichen Geschwindigkeiten bewegen?
A: Nach der speziellen Relativitätstheorie verlangsamt sich die Zeit für ein Objekt umso mehr, je schneller es sich bewegt. Für das langsamere Objekt vergeht die Zeit schneller als für das sehr schnelle Objekt, was bedeutet, dass die Zeit für sie viel langsamer vergeht.
F: Was passiert, wenn ein Objekt die Lichtgeschwindigkeit erreicht?
A: Wenn ein Objekt die Lichtgeschwindigkeit erreicht, liegt es auf der t-Achse bei Null, was bedeutet, dass es in der Zeitrichtung keinen Fortschritt gemacht hat. Das bedeutet, dass die Zeit für den Beobachter stehen bleibt.
F: In welchen Bereichen werden Weltlinien verwendet?
A: Weltlinien werden sehr häufig in der theoretischen Physik und der speziellen sowie der allgemeinen Relativitätstheorie verwendet.
F: Wie können wir uns eine Weltlinie vorstellen?
A: Wir können eine Weltlinie visualisieren, indem wir uns Illustrationen ansehen, die zeigen, wie Objekte, die sich mit unterschiedlichen Geschwindigkeiten fortbewegen, unterschiedlich schnell die Zeit vergehen lassen.
F: Gibt es eine Möglichkeit, eine einmal festgelegte Weltlinie zu ändern oder zu ergänzen?
A: Sobald eine Weltlinie festgelegt ist, kann sie nicht mehr verändert werden, da sie einen unveränderlichen Pfad durch die Raumzeit darstellt.
F: Worauf bezieht sich die "t-Achse" in Bezug auf das Erreichen der Lichtgeschwindigkeit? A: Die "t-Achse" bezieht sich auf den Fortschritt in Bezug auf die Zeit - wenn ein Objekt die Lichtgeschwindigkeit erreicht, ist sein Fortschritt in Bezug auf die Zeit auf dieser Achse gleich Null, was bedeutet, dass kein Fortschritt in Bezug auf das Passieren der Raumzeit gemacht wurde.
Suche in der Enzyklopädie

