Skalarprodukt

In der Mathematik ist das Punktprodukt eine Operation, die zwei Vektoren als Eingabe nimmt und als Ausgabe eine skalare Zahl liefert. Die zurückgegebene Zahl hängt von der Länge der beiden Vektoren und vom Winkel zwischen ihnen ab. Der Name leitet sich von dem zentrierten Punkt "-" ab, der oft zur Bezeichnung dieser Operation verwendet wird; der alternative Name Skalarprodukt betont die skalare (und nicht die vektorielle) Natur des Ergebnisses.

Das Punktprodukt kontrastiert (im dreidimensionalen Raum) mit dem Kreuzprodukt, das als Ergebnis einen Vektor erzeugt.

Definition

Das Punktprodukt zweier Vektoren a = [a1, a2, ..., _an] und b = [b1, b2, ..., bn] ist definiert als:

a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}}} $\mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}$

wobei Σ die Summationsnotation (die Summe aller Terme) und n die Dimension des Vektorraums bezeichnet.

In der Dimension 2 ist das Punktprodukt der Vektoren [a,b] und [c,d] ac + bd. In gleicher Weise ist in einer Dimension 3 das Punktprodukt der Vektoren [a,b,c] und [d,e,f] ad + be + cf. Zum Beispiel ist das Punktprodukt zweier dreidimensionaler Vektoren [1, 3, -5] und [4, -2, -1]

[ 1 , 3 , − 5 ] ⋅ [ 4 , − 2 , − 1 ] = ( 1 × 4 ) + ( 3 × ( − 2 ) ) + ( ( ( - 5 ) × ( - 1 ) ) = ( 4 ) - ( 6 ) + ( 5 ) = 3. {\Anzeigestil [1,3,-5]\cdot [4,-2,-1]=(1\mal 4)+(3\mal (-2))+((-5)\mal (-1))=(4)-(6)+(5)=3.} $[1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.$

Geometrische Interpretation

In der euklidischen Geometrie stehen das Punktprodukt, die Länge und der Winkel in Beziehung zueinander. Für einen Vektor a ist das Punktprodukt a - a das Quadrat der Länge von a, oder

a ⋅ a = ‖ a ‖ 2 {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=\links\|\mathbf {a} \rechts\|^{2}} ${\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}$

wobei ||a||| die Länge (Größe) von a bezeichnet. Allgemeiner ausgedrückt, wenn b ein anderer Vektor ist

a ⋅ b = ‖ a ‖ ‖ b ‖ cos θ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|\cos \theta \,} $\mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|\cos \theta \,$

wobei ||a||| und ||b||| die Länge von a und b bezeichnen und θ der Winkel zwischen ihnen ist.

Diese Formel kann umgestellt werden, um die Größe des Winkels zwischen zwei Nicht-Null-Vektoren zu bestimmen:

θ = arccos ( a ⋅ b ‖ a ‖ ‖ b ‖ ) {\displaystyle \theta =\arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}}}right\|\left\|{\mathbf {b}}}right\|{\mathbf {b}}}}right}}} $\theta =\arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}\right\|}}\right)$

Man kann die Vektoren auch zunächst in Einheitsvektoren umrechnen, indem man sie durch ihre Größe dividiert:

a ^ = a ‖ a ‖ {\displaystyle {\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}} ${\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}$

dann ist der Winkel θ gegeben durch

θ = arccos ( a ^ ⋅ b ^ ) {\displaystyle \theta =\arccos({\boldsymbol {\hat {\hat {a}}}\cdot {\boldsymbol {\hat {\hat {b}}})} $\theta =\arccos({\boldsymbol {\hat {a}}}\cdot {\boldsymbol {\hat {b}}})$

Da der Kosinus von 90° Null ist, ist das Punktprodukt zweier orthogonaler (senkrechter) Vektoren immer Null. Darüber hinaus können zwei Vektoren als orthogonal betrachtet werden, wenn und nur wenn ihr Punktprodukt Null ist und beide eine Länge ungleich Null haben. Diese Eigenschaft bietet eine einfache Methode zum Testen der Bedingung der Orthogonalität.

Manchmal werden diese Eigenschaften auch zur Definition des Punktprodukts verwendet, insbesondere in 2- und 3-Dimensionen; diese Definition entspricht der obigen. Für höhere Dimensionen kann die Formel verwendet werden, um den Begriff des Winkels zu definieren.

Die geometrischen Eigenschaften beruhen darauf, dass die Basis orthonormal ist, d.h. aus paarweise senkrechten Vektoren mit Einheitslänge besteht.

Skalare Projektion

Wenn sowohl a als auch b die Länge eins haben (d.h. Einheitsvektoren sind), gibt ihr Punktprodukt einfach den Kosinus des Winkels zwischen ihnen an.

Wenn nur b ein Einheitsvektor ist, dann ergibt das Punktprodukt a - b |a| cos(θ), d.h. den Betrag der Projektion von a in Richtung b, mit einem Minuszeichen, wenn die Richtung entgegengesetzt ist. Man nennt dies die skalare Projektion von a auf b oder die skalare Komponente von a in Richtung b (siehe Abbildung). Diese Eigenschaft des Punktprodukts hat mehrere nützliche Anwendungen (zum Beispiel, siehe nächster Abschnitt).

Wenn weder a noch b ein Einheitsvektor ist, dann wäre die Größe der Projektion von a in Richtung b z.B. a - (b / |b|), da der Einheitsvektor in Richtung b b / |b| ist.

Rotation

Eine Drehung der orthonormalen Basis, nach der der Vektor a dargestellt wird, erhält man durch eine Multiplikation von a mit einer Rotationsmatrix R. Diese Matrixmultiplikation ist nur eine kompakte Darstellung einer Folge von Punktprodukten.

Lassen Sie zum Beispiel

_B1 = {x, y, z} und _B2 = {u, v, w} sind zwei verschiedene orthonormale Basen desselben Raumes ^R3, wobei _B2 durch einfaches Drehen von _B1 erhalten wird,
a1 = (_ax, ay, az) stellen den Vektor a in Bezug auf _B1 dar,
a2 = (_au, _av, _aw) stellen denselben Vektor in Bezug auf die rotierte Basis _B2 dar,
u1, v1, w1 sind die rotierten Basisvektoren u, v, w, die durch _B1 repräsentiert werden.

Dann wird die Rotation von _B1 nach _B2 wie folgt durchgeführt:

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}\\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}={\beginnt{beginnt}a_{u}\\\a_{v}\\a_{w}\end{bmatrix}}. } ${\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\\a_{v}\\a_{w}\end{bmatrix}}.$

Beachten Sie, dass die Rotationsmatrix R unter Verwendung der gedrehten Basisvektoren u1, v1, w1 als ihre Zeilen zusammengesetzt wird, und diese Vektoren sind Einheitsvektoren. Per Definition besteht Ra1 aus einer Folge von Punktprodukten zwischen jeder der drei Reihen von R und dem Vektor a1. Jedes dieser Punktprodukte bestimmt eine skalare Komponente von a in Richtung eines gedrehten Basisvektors (siehe voriger Abschnitt).

Wenn a1 nicht ein Spaltenvektor, sondern ein Zeilenvektor ist, dann muss R die gedrehten Basisvektoren in seinen Spalten enthalten und a1 nachmultiplizieren:

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x u y v y w y u z v z w z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\anfang{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}={\begin{bmatrix}{\mathbf {u}}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}}_{1}\cdot {\mathbf {a}}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}. } ${\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}.$

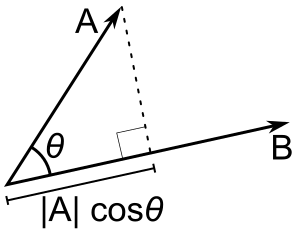
A - B = |A| |B| cos(θ). |A| cos(θ) ist die skalare Projektion von A auf B.

Physik

In der Physik ist die Grösse ein Skalar im physikalischen Sinne, d.h. eine vom Koordinatensystem unabhängige physikalische Grösse, ausgedrückt als Produkt aus einem Zahlenwert und einer physikalischen Einheit, nicht nur einer Zahl. Auch das Punktprodukt ist ein Skalar in diesem Sinne, gegeben durch die Formel, unabhängig vom Koordinatensystem. Beispiel:

Mechanische Arbeit ist das Punktprodukt von Kraft- und Verschiebungsvektoren.
Der magnetische Fluss ist das Punktprodukt aus dem Magnetfeld und den Flächenvektoren.
Die volumetrische Durchflussmenge ist das Punktprodukt der Fluidgeschwindigkeit und der Flächenvektoren.

Eigenschaften

Die folgenden Eigenschaften gelten, wenn a, b und c reelle Vektoren sind und r ein Skalar ist.

Das Punktprodukt ist kommutativ:

a ⋅ b = b ⋅ a . {\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} . } $\mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} .$

Das Punktprodukt ist distributiv über die Vektoraddition:

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {\darstellungsstil \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} . } $\mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} .$

Das Punktprodukt ist bilinear:

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) . {\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ). } $\mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ).$

Wenn es mit einem skalaren Wert multipliziert wird, ist das Punktprodukt zufriedenstellend:

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}\c_{2})(\mathbf {a} \cdot \mathbf {b} )} $(c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )$

(diese letzten beiden Eigenschaften folgen aus den ersten beiden).

Zwei Nicht-Null-Vektoren a und b sind dann und nur dann senkrecht, wenn a - b = 0.

Im Gegensatz zur Multiplikation gewöhnlicher Zahlen, bei der, wenn ab = ac, dann b immer gleich c ist, es sei denn, a ist Null, gehorcht das Punktprodukt nicht dem Löschungsgesetz:

Wenn a - b = a - c und a ≠ 0, dann können wir schreiben: a - (b - c) = 0 nach dem Verteilungsgesetz; das obige Ergebnis besagt, dass dies nur bedeutet, dass a senkrecht zu (b - c) steht, was immer noch (b - c) ≠ 0, und somit b ≠ c erlaubt.

Vorausgesetzt, dass die Basis orthonormal ist, ist das Punktprodukt invariant bei isometrischen Änderungen der Basis: Rotationen, Reflexionen und Kombinationen, wobei der Ursprung fixiert bleibt. Die oben erwähnte geometrische Interpretation stützt sich auf diese Eigenschaft. Mit anderen Worten, für einen orthonormalen Raum mit einer beliebigen Anzahl von Dimensionen ist das Punktprodukt unter einer Koordinatentransformation auf der Grundlage einer orthogonalen Matrix invariant. Dies entspricht den beiden folgenden Bedingungen:

Die neue Basis ist wieder orthonormal (d.h. sie ist orthonormal ausgedrückt in der alten).
Die neuen Basisvektoren haben die gleiche Länge wie die alten (d.h. Einheitslänge in Bezug auf die alte Basis).

Wenn a und b Funktionen sind, dann ist die Ableitung von a - b a' - b + a - b'

Dreifache Produkterweiterung

Dies ist eine sehr nützliche Identität (auch bekannt als Lagrangesche Formel), die die Punkt- und Kreuzprodukte umfasst. Sie wird geschrieben als

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) {\darstellungsstil \mathbf {a} {\mathbf {b} \mal (\mathbf {b} \mal \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} {b} } $\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )$

der leichter als "BAC minus CAB" zu merken ist, wenn man sich vor Augen hält, welche Vektoren punktiert sind. Diese Formel wird häufig zur Vereinfachung von Vektorberechnungen in der Physik verwendet.

Nachweis der geometrischen Interpretation

Betrachten Sie das Element von Rn

v = v 1 e ^ 1 + v 2 e ^ 2 + . . . + v n e ^ n . {\Anzeigestil \mathbf {v} =v_{1}\mathbf {\hat {\e}} _{1}+v_{2}\mathbf {\hat {\hat}} {2}+...+v_{n}\mathbf {\an8}das {\an8} _{n}.\,} $\mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,$

Wiederholte Anwendung des Satzes des Pythagoras ergibt für seine Länge |v|

| v | 2 = v 1 2 + v 2 2 2 + . . . + v n 2 2 . {\Anzeigestil |\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,} $|\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,$

Aber das ist dasselbe wie

v ⋅ v = v 1 2 + v 2 2 2 + . . . + v n 2 , {\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,} $\mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,$

Wir kommen also zu dem Schluss, dass man, wenn man das Punktprodukt eines Vektors v mit sich selbst nimmt, die quadrierte Länge des Vektors erhält.

Lemma 1

v ⋅ v = | v | 2 . {\Anzeigestil \mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,} $\mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,$

Betrachten Sie nun zwei Vektoren a und b, die vom Ursprung ausgehen, getrennt durch einen Winkel θ. Ein dritter Vektor c kann definiert werden als

c = d e f a - b . {\Anzeigestil \mathbf {c} \ {\ \ \ {\ \ {\ {\}Mathrm {\} {}{=}}\mathbf {a} -\mathbf {b} .\,} $\mathbf {c} \ {\stackrel {\mathrm {def} }{=}}\ \mathbf {a} -\mathbf {b} .\,$

die ein Dreieck mit den Seiten a, b und c bilden. Nach dem Kosinusgesetz haben wir

| c | 2 = | a | 2 + | b | 2 - 2 | a | | | b | cos θ . {\Anzeigestil |\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\{\mathbf {b} |\{\cos \cos \theta \,} $|\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

Ersetzt man die quadrierten Längen nach Lemma 1 durch Punktprodukte, so erhält man

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | | | b | cos θ . {\Anzeigestil \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\{\mathbf {b} |\cos \theta .\,} $\mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$ (1)

Aber als c ≡ a - b, haben wir auch

c ⋅ c = ( a - b ) ⋅ ( a - b ) {\displaystyle \mathbf {c} \cdot \mathbf {c} = (\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,} $\mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,$ ,

die sich nach dem Verteilungsgesetz ausdehnt auf

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) . {\Anzeigestil \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,} $\mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,$ (2)

Wenn man die beiden c - c-Gleichungen (1) und (2) zusammenführt, erhält man

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | | | b | cos θ . {\Anzeigestil \mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\{\mathbf {b} |\{\cos \cos \theta \,} $\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

a - a + b - b von beiden Seiten subtrahieren und durch -2 Blätter teilen

a ⋅ b = | a | | | b | cos θ . {\darstellungsstil \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\{\mathbf {b} |\{\cos \cos \theta \,} $\mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

FRAGE UND ANTWORT.

Verallgemeinerung

Das innere Produkt verallgemeinert das Punktprodukt zu abstrakten Vektorräumen und wird üblicherweise mit ⟨ a , b ⟩ {\displaystyle \langle \mathbf {a} \,,\mathbf {b} bezeichnet. \Rangel } $\langle \mathbf {a} \,,\mathbf {b} \rangle$ . Aufgrund der geometrischen Interpretation des Punktprodukts ist die Norm ||a||| eines Vektors a in einem solchen inneren Produktraum definiert als

‖ a ‖ = ⟨ a , a ⟩ {\displaystyle \|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }} $\|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}$

so dass es die Länge verallgemeinert, und den Winkel θ zwischen zwei Vektoren a und b durch

cos θ = ⟨ a , b ⟩ ‖ a ‖ ‖ b ‖ . {\displaystyle \cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \rangle {\|\mathbf {a} \|\,\|\mathbf {b} \|}}. } $\cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \rangle }{\|\mathbf {a} \|\,\|\mathbf {b} \|}}.$

Insbesondere werden zwei Vektoren als orthogonal betrachtet, wenn ihr inneres Produkt Null ist

⟨ a , b ⟩ = 0. {\Darstellungsstil \langle \mathbf {a} \,,\mathbf {b} \Rangel =0.} $\langle \mathbf {a} \,,\mathbf {b} \rangle =0.$

Bei Vektoren mit komplexen Einträgen würde die Verwendung der gegebenen Definition des Punktprodukts zu ganz anderen geometrischen Eigenschaften führen. Beispielsweise kann das Punktprodukt eines Vektors mit sich selbst eine beliebige komplexe Zahl sein, und es kann Null sein, ohne dass der Vektor der Nullvektor ist; dies wiederum hätte schwerwiegende Folgen für Begriffe wie Länge und Winkel. Viele geometrische Eigenschaften können um den Preis der Aufgabe der symmetrischen und bilinearen Eigenschaften des Skalarproduktes gerettet werden, indem alternativ

a ⋅ b = ∑ a i b i ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}} $\mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}$

wobei _bi das komplexe Konjugat von _bi ist. Dann ist das Skalarprodukt jedes Vektors mit sich selbst eine nicht-negative reelle Zahl, und sie ist mit Ausnahme des Null-Vektors ungleich Null. Allerdings ist dieses Skalarprodukt in b nicht linear (sondern eher konjugiert linear), und das Skalarprodukt ist auch nicht symmetrisch, da

a ⋅ b = b ⋅ a ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}} $\mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}$ .

Diese Art von Skalarprodukt ist dennoch recht nützlich und führt zu den Begriffen der hermitianischen Form und der allgemeinen inneren Produkträume.

Das innere Produkt von Frobenius verallgemeinert das Punktprodukt zu Matrizen. Es ist definiert als die Summe der Produkte der entsprechenden Komponenten von zwei Matrizen gleicher Größe.

Verallgemeinerung auf Tensoren

Das Punktprodukt zwischen einem Tensor der Ordnung n und einem Tensor der Ordnung m ist ein Tensor der Ordnung n+m-2. Das Punktprodukt wird durch Multiplikation und Summierung über einen einzigen Index in beiden Tensoren berechnet. Wenn A {\darstellungsstil \mathbf {A} } $\mathbf {A}$ und B {\darstellungsstil \mathbf {B} } $\mathbf {B}$ sind zwei Tensoren mit Elementdarstellung A i j ... k ℓ ... {\darstellungsstil A_{ij\dots }^{k\ell \dots }} $A_{ij\dots }^{k\ell \dots }$ und B m n ... p ... i {\darstellungsstil B_{mn\dots }^{p{\dots }i}} $B_{mn\dots }^{p{\dots }i}$ die Elemente des Punktprodukts A ⋅ B {\darstellungsstil \mathbf {A} \cdot \mathbf {B} } $\mathbf {A} \cdot \mathbf {B}$ sind gegeben durch

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ℓ ... B m n ... p ... i {\Darstellungsstil A_{ij\Punkte ^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}} $A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}$

Diese Definition reduziert sich natürlich auf das Standard-Vektorpunktprodukt, wenn sie auf Vektoren angewendet wird, und auf die Matrix-Multiplikation, wenn sie auf Matrizen angewendet wird.

Gelegentlich wird ein Doppelpunktprodukt verwendet, um das Multiplizieren und Summieren über zwei Indizes darzustellen. Das Doppelpunktprodukt zwischen zwei Tensoren 2. Ordnung ist ein Skalar.

Fragen und Antworten

Q: What is the dot product in mathematics?

A: The dot product is an operation that takes two vectors as input and returns a scalar number as output.

Q: What does the dot product depend on?

A: The dot product depends on the length of both vectors and on the angle between them.

Q: Why is the name of the dot product derived from the centered dot "·"?

A: The name is derived from the centered dot "·" that is often used to designate this operation.

Q: What is the alternative name for the dot product?

A: The alternative name is scalar product, which emphasizes the scalar (rather than vector) nature of the result.

Q: What is the contrast between the dot product and the cross product in three-dimensional space?

A: The dot product produces a scalar number as result, while the cross product produces a vector as result.

Q: What is the dot product used for in mathematics?

A: The dot product can be used to determine if two vectors are perpendicular (have an angle of 90 degrees), and to project one vector onto another.

Q: Can the dot product be used in higher-dimensional spaces?

A: Yes, the dot product can be extended to higher-dimensional spaces by generalizing the definition.