Logarithmische Darstellung
Eine logarithmische Skala ist eine Skala, die verwendet wird, wenn es einen großen Mengenbereich gibt. Häufige Anwendungsbereiche sind Erdbebenstärke, Schallintensität, Lichtintensität und pH-Wert von Lösungen.
Sie basiert auf Größenordnungen und nicht auf einer linearen Standardskala. Der Wert jeder Markierung auf der Skala ist der Wert an der vorherigen Markierung multipliziert mit einer Konstanten.
Logarithmische Skalen werden auch in Rechenschiebern zum Multiplizieren oder Dividieren von Zahlen durch Addieren oder Subtrahieren von Längen auf den Skalen verwendet.
Die logarithmische Skala kann hilfreich sein, wenn die Daten einen großen Wertebereich abdecken - der Logarithmus reduziert dies auf einen überschaubareren Bereich.
Einige unserer Sinne arbeiten auf logarithmische Weise (die Multiplikation der tatsächlichen Eingangsstärke addiert eine Konstante zur wahrgenommenen Signalstärke, siehe Stevens'sches Leistungsgesetz). Das macht logarithmische Skalen für diese Eingangsgrößen besonders geeignet. Insbesondere nimmt unser Gehör gleiche Vielfache von Frequenzen als gleiche Unterschiede in der Tonhöhe wahr.
Auf den meisten logarithmischen Skalen entsprechen kleine Vielfache (oder Verhältnisse) der zugrunde liegenden Größe kleinen (möglicherweise negativen) Werten des logarithmischen Maßes.
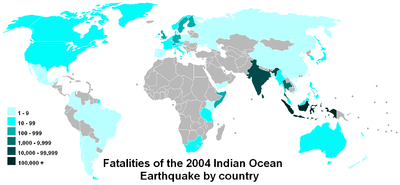
Eine Log-Skala erleichtert den Vergleich von Werten, die einen großen Bereich abdecken, wie in dieser Karte
Die beiden logarithmischen Skalen eines Rechenschiebers
Beispiele
Bekannte Beispiele für solche Skalen sind:
- Richter-Magnitudenskala und Momentmagnitudenskala (MMS) für die Stärke von Erdbeben und Bewegungen in der Erde.
- bel und Dezibel und Neper für akustische Leistung (Lautheit) und elektrische Leistung;
- Zählen von Blendenstufen für die Verhältnisse der fotografischen Belichtung;
- Bewertung niedriger Wahrscheinlichkeiten durch die Anzahl von "Neunen" in der Dezimalexpansion der Wahrscheinlichkeit, dass sie nicht eintreten: ein System, das mit einer Wahrscheinlichkeit von 10-5 versagen wird, ist beispielsweise zu 99,999% zuverlässig: "fünf Neunen".
- Entropie in der Thermodynamik.
- Information in der Informationstheorie.
- Korngrößenverteilungskurven des Bodens
Einige logarithmische Skalen wurden so gestaltet, dass große Werte (oder Verhältnisse) der zugrunde liegenden Größe kleinen Werten des logarithmischen Maßes entsprechen. Beispiele für solche Skalen sind:
- pH-Wert für Säuregehalt;
- stellare Magnitudenskala für die Helligkeit von Sternen;
Eine logarithmische Skala ist auch eine grafische Skala auf einer oder beiden Seiten eines Diagramms, bei der eine Zahl x in einem Abstand c-log(x) von dem mit der Zahl 1 markierten Punkt aufgedruckt ist. Ein Rechenschieber hat logarithmische Skalen, und Nomogramme verwenden oft logarithmische Skalen. Auf einer logarithmischen Skala wird ein gleicher Unterschied in der Größenordnung durch einen gleichen Abstand dargestellt. Das geometrische Mittel zweier Zahlen liegt auf halbem Weg zwischen den Zahlen.
Logarithmisches Millimeterpapier war vor dem Aufkommen der Computergrafik ein grundlegendes wissenschaftliches Werkzeug. Diagramme auf Papier mit einer logarithmischen Skala können Exponentialgesetze und auf logarithmischem Papier Potenzgesetze als gerade Linien darstellen (siehe Semilogarithmische Grafik, logarithmische Grafik).
Fragen und Antworten
F: Was ist eine logarithmische Skala?
A: Eine logarithmische Skala ist eine Skala, die verwendet wird, wenn es einen großen Bereich von Mengen gibt.
F: Was sind einige Beispiele für Dinge, die auf einer logarithmischen Skala gemessen werden können?
A: Die Stärke von Erdbeben, die Lautstärke von Geräuschen, die Lichtintensität, die Ausbreitungsgeschwindigkeit von Epidemien und der pH-Wert von Lösungen können alle auf einer logarithmischen Skala gemessen werden.
F: Wie unterscheidet sich eine logarithmische Skala von einer linearen Standardskala?
A: Eine logarithmische Skala basiert auf Größenordnungen und nicht auf einer linearen Standardskala. Der Wert jeder Markierung auf der Skala ist der Wert der vorherigen Markierung multipliziert mit einer Konstante.
F: Welchen Vorteil hat die Verwendung einer logarithmischen Skala?
A: Die logarithmische Skala kann einen großen Wertebereich auf einen überschaubareren Bereich reduzieren, was hilfreich sein kann, wenn Sie mit Daten zu tun haben, die eine große Bandbreite an Werten umfassen.
F: Was ist das Stevens'sche Potenzgesetz und wie verhält es sich zu logarithmischen Skalen?
A: Das Stevens'sche Potenzgesetz beschreibt, wie einige unserer Sinne auf logarithmische Weise funktionieren, wobei die Multiplikation der tatsächlichen Eingangsstärke eine Konstante zur wahrgenommenen Signalstärke hinzufügt. Das macht logarithmische Skalen für diese Eingangsgrößen besonders geeignet.
F: Warum ist eine logarithmische Skala besonders nützlich für die Messung der Lautstärke von Geräuschen?
A: Unser Gehör nimmt gleiche Vielfache von Frequenzen als gleiche Unterschiede in der Tonhöhe wahr, so dass eine logarithmische Skala diese Beziehung zwischen Tonfrequenz und wahrgenommener Lautstärke genau darstellen kann.
F: Wie ist das Verhältnis zwischen kleinen Vielfachen der zugrunde liegenden Größe und dem logarithmischen Maß auf den meisten logarithmischen Skalen?
A: Bei den meisten logarithmischen Skalen entsprechen kleine Vielfache (oder Verhältnisse) der zugrunde liegenden Größe kleinen (möglicherweise negativen) Werten des logarithmischen Maßes.
Suche in der Enzyklopädie