Oberflächenintegral

In der Mathematik ist ein Flächenintegral ein definitives Integral, das über eine Fläche (die eine im Raum gesetzte Kurve sein kann) gebildet wird. So wie ein Linienintegral eine Dimension oder eine Variable behandelt, kann man sich ein Flächenintegral als Doppelintegral entlang zweier Dimensionen vorstellen. Bei einer Fläche kann man über ihre skalaren Felder (d.h. Funktionen, die Zahlen als Werte zurückgeben) und Vektorfelder (d.h. Funktionen, die Vektoren als Werte zurückgeben) integrieren.

Oberflächenintegrale haben Anwendungen in der Physik, insbesondere mit der klassischen Theorie des Elektromagnetismus.

Die Definition des Oberflächenintegrals beruht auf der Zerlegung der Oberfläche in kleine Flächenelemente.

Eine Illustration eines einzelnen Oberflächenelements. Diese Elemente werden durch den Begrenzungsvorgang infinitesimal klein gemacht, um sich der Oberfläche anzunähern.

Oberflächenintegrale von Skalarfeldern

Betrachten Sie eine Fläche S, auf der ein Skalarfeld f definiert ist. Wenn man sich S als aus irgendeinem Material bestehend vorstellt und für jedes x in S die Zahl f(x) die Dichte des Materials bei x ist, dann ist das Oberflächenintegral von f über S die Masse pro Einheitsdicke von S. (Dies gilt nur, wenn die Oberfläche eine unendlich dünne Schale ist.) Ein Ansatz zur Berechnung des Oberflächenintegrals besteht dann darin, die Oberfläche in viele sehr kleine Stücke zu zerteilen, anzunehmen, dass auf jedem Stück die Dichte annähernd konstant ist, die Masse pro Dickeneinheit jedes Stücks zu ermitteln, indem die Dichte des Stücks mit seiner Fläche multipliziert wird, und dann die sich ergebenden Zahlen zu addieren, um die Gesamtmasse pro Dickeneinheit von S zu ermitteln.

Um eine explizite Formel für das Oberflächenintegral zu finden, parametrisieren Mathematiker S, indem sie auf S ein System von krummlinigen Koordinaten betrachten, wie den Längen- und Breitengrad auf einer Kugel. Eine solche Parametrisierung sei x(s, t), wobei (s, t) in einem Bereich T in der Ebene variiert. Dann ist das Oberflächenintegral gegeben durch

∫ S f d S = ∬ T f ( x ( s , t ) ) | ∂ x ∂ s × ∂ x ∂ t | d s d t {\displaystyle \int _{S}f\,dS=\iint _{T}f(\mathbf {x} (s,t))\links|{\teilweise \mathbf {x} \über \teilweise s}\mal {\teilweise \mathbf {x} \über \teilweise t}\rechts},dt} $\int _{S}f\,dS=\iint _{T}f(\mathbf {x} (s,t))\left|{\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right|ds\,dt$

wobei der Ausdruck zwischen den Balken auf der rechten Seite die Grösse des Kreuzprodukts der partiellen Ableitungen von x(s, t) ist.

Um zum Beispiel die Oberfläche einer allgemeinen funktionellen Form zu finden, sagen wir z = f ( x , y ) {\darstellungsstil z=f\,(x,y)} $z=f\,(x,y)$ haben wir

A = ∫ S d S = ∬ T ‖ ∂ r ∂ x × ∂ r ∂ y ‖ d x d y {\displaystyle A=\int _{S}\,dS=\iint _{T}\left\|{\teilweise \mathbf {r} \über \teilweise x}\mal {\teilweise \mathbf {r} \über \teilweise y}\right\|dx\,dy} $A=\int _{S}\,dS=\iint _{T}\left\|{\partial \mathbf {r} \over \partial x}\times {\partial \mathbf {r} \over \partial y}\right\|dx\,dy$

wobei r = ( x , y , z ) = ( x , y , f ( x , y ) ) {\Anzeigestil \mathbf {r} =(x,y,z)=(x,y,f(x,y))} $\mathbf {r} =(x,y,z)=(x,y,f(x,y))$ . So dass ∂ r ∂ x = ( 1 , 0 , f x ( x , y ) ) Darstellungsstil {\teilweise \mathbf {r} \über \teilweise x}=(1,0,f_{x}(x,y))} ${\partial \mathbf {r} \over \partial x}=(1,0,f_{x}(x,y))$ , und ∂ r ∂ y = ( 0 , 1 , f y ( x , y ) ) Darstellungsstil {\teilweise \mathbf {r} \über \teilweise y}=(0,1,f_{y}(x,y))} ${\partial \mathbf {r} \over \partial y}=(0,1,f_{y}(x,y))$ . So,

A = ∬ T ‖ ( 1 , 0 , ∂ f ∂ x ) × ( 0 , 1 , ∂ f ∂ x ) × ( 0 , 1 , ∂ f ∂ y ) ‖ d x d y = ∬ T ‖ ( - ∂ f ∂ x , - ∂ f ∂ y , 1 ) ‖ d x d y = ∬ T ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 + 1 d x d y {\Darstellungsstil {\beginnt{beginnt}A&{}=\iint _{{T}\links\|\links(1,0,{\teilweise f \über \teilweise x}\rechts)\mal \links(0,1,{\teilweise f \über \teilweise y}\rechts)\rechts\|dx\,dy\\&{}=\iint _{T}\left\|\left(-{\teilweise f \über \teilweise x},-{\teilweise f \über \teilweise y},1\right)\right\|dx\,dy\\\&{}=\iint _{{T}{\sqrt {\links ({\teilweise f \über \teilweise x}\rechts)^{2}+\links ({\teilweise f \über \teilweise y}\rechts)^{2}+1}}\,\,dx\,dy\end{ausgerichtet}} ${\begin{aligned}A&{}=\iint _{T}\left\|\left(1,0,{\partial f \over \partial x}\right)\times \left(0,1,{\partial f \over \partial y}\right)\right\|dx\,dy\\&{}=\iint _{T}\left\|\left(-{\partial f \over \partial x},-{\partial f \over \partial y},1\right)\right\|dx\,dy\\&{}=\iint _{T}{\sqrt {\left({\partial f \over \partial x}\right)^{2}+\left({\partial f \over \partial y}\right)^{2}+1}}\,\,dx\,dy\end{aligned}}$

das ist die Formel, die für die Oberfläche einer allgemeinen funktionellen Form verwendet wird. Man kann den Vektor in der zweiten Zeile oben als den Normalenvektor zur Oberfläche erkennen.

Beachten Sie, dass aufgrund des Vorhandenseins des Kreuzprodukts die obigen Formeln nur für Oberflächen funktionieren, die in den dreidimensionalen Raum eingebettet sind.

Oberflächenintegrale von Vektorfeldern

Betrachten Sie ein Vektorfeld v auf S, d.h. für jedes x in S ist v(x) ein Vektor.

Das Oberflächenintegral kann komponentenweise entsprechend der Definition des Oberflächenintegrals eines Skalarfeldes definiert werden; das Ergebnis ist ein Vektor. Dies gilt z.B. für das elektrische Feld an einem festen Punkt aufgrund einer elektrisch geladenen Oberfläche oder für die Schwerkraft an einem festen Punkt aufgrund einer Materialplatte. Es kann auch der magnetische Fluss durch eine Oberfläche berechnet werden.

Alternativ können Mathematiker die Normalkomponente des Vektorfeldes integrieren; das Ergebnis ist ein Skalar. Ein Beispiel ist ein Fluid, das durch S fließt, so dass v(x) die Geschwindigkeit des Fluids bei x bestimmt. Der Fluss ist definiert als die Menge des Fluids, die durch S in einer Zeiteinheit fließt.

Diese Illustration impliziert, dass, wenn das Vektorfeld an jedem Punkt tangential zu S ist, der Fluss null ist, weil das Fluid einfach parallel zu S fließt und weder hinein noch heraus. Dies impliziert auch, dass, wenn v nicht nur entlang S fließt, d.h. wenn v sowohl eine tangentiale als auch eine normale Komponente hat, dann trägt nur die normale Komponente zum Fluss bei. Ausgehend von dieser Argumentation müssen wir, um den Fluss zu finden, das Punktprodukt von v mit der Einheitsfläche senkrecht zu S an jedem Punkt nehmen, was uns ein skalares Feld ergibt, und das erhaltene Feld wie oben beschrieben integrieren. Dies ergibt die Formel

∫ S v ⋅ d S = ∫ S ( v ⋅ n ) d S = ∬ T v ( x ( s , t ) ) ⋅ ( ∂ x ∂ s × ∂ x ∂ t ) d s d t . {\Anzeigestil \int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }=\int _{S}({\mathbf {v} }cdot {\mathbf {n} })\,dS=\iint _{{T}{\mathbf {v} }(\mathbf {x} (s,t))\cdot \left({\teilweise \mathbf {x} \über \teilweise s}\mal {\teilweise \mathbf {x} \über \teilweise t}\rechts)ds\,dt. } $\int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }=\int _{S}({\mathbf {v} }\cdot {\mathbf {n} })\,dS=\iint _{T}{\mathbf {v} }(\mathbf {x} (s,t))\cdot \left({\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right)ds\,dt.$

Das Kreuzprodukt auf der rechten Seite dieses Ausdrucks ist eine durch die Parametrisierung bestimmte Flächennormale.

Diese Formel definiert das Integral auf der linken Seite (beachten Sie den Punkt und die Vektornotation für das Oberflächenelement).

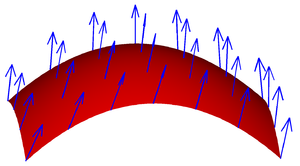
Ein Vektorfeld auf einer Oberfläche.

Theoreme mit Oberflächenintegralen

Verschiedene nützliche Ergebnisse für Oberflächenintegrale können mit Hilfe der Differentialgeometrie und der Vektorrechnung, wie dem Divergenztheorem, und seiner Verallgemeinerung, dem Stokes'schen Satz, abgeleitet werden.

Fortgeschrittene Fragen

Ändern der Parametrisierung

In der obigen Diskussion wurde das Oberflächenintegral definiert, indem eine Parametrisierung der Oberfläche S verwendet wurde. Wenn z.B. die Positionen des Nordpols und des Südpols auf einer Kugel verschoben werden, ändern sich die Breiten- und Längengrade für alle Punkte auf der Kugel. Eine natürliche Frage ist dann, ob die Definition des Oberflächenintegrals von der gewählten Parametrisierung abhängt. Für Integrale skalarer Felder ist die Antwort auf diese Frage einfach: Der Wert des Oberflächenintegrals ist unabhängig von der gewählten Parametrisierung immer gleich.

Integrale von Vektorfeldern sind komplizierter, da die Oberflächennormale beteiligt ist. Mathematiker haben bewiesen, dass bei zwei Parametrisierungen der gleichen Oberfläche, deren Oberflächennormalen in die gleiche Richtung zeigen, beide Parametrisierungen den gleichen Wert für das Oberflächenintegral ergeben. Wenn jedoch die Normalen für diese Parametrisierungen in entgegengesetzte Richtungen zeigen, ist der Wert des mit einer Parametrisierung erhaltenen Flächenintegrals der negative Wert des mit der anderen Parametrisierung erhaltenen Flächenintegrals. Daraus folgt, dass wir uns bei einer gegebenen Oberfläche nicht an irgendeine eindeutige Parametrisierung halten müssen; aber bei der Integration von Vektorfeldern müssen wir im Voraus entscheiden, in welche Richtung die Normale zeigen wird, und dann irgendeine Parametrisierung wählen, die mit dieser Richtung übereinstimmt.

Parametrisierungen arbeiten auf Teilen der Oberfläche

Ein weiteres Problem ist, dass Oberflächen manchmal keine Parametrisierungen haben, die die gesamte Oberfläche abdecken; dies gilt zum Beispiel für die Oberfläche eines Zylinders (von endlicher Höhe). Die offensichtliche Lösung besteht dann darin, diese Oberfläche in mehrere Teile zu teilen, das Flächenintegral auf jedem Teil zu berechnen und dann alle zusammen zu addieren. So funktionieren die Dinge in der Tat, aber bei der Integration von Vektorfeldern muss man wieder vorsichtig sein, wie man den Normalenvektor für jedes Stück der Oberfläche wählt, so dass die Ergebnisse konsistent sind, wenn die Stücke wieder zusammengesetzt werden. Für den Zylinder bedeutet dies, dass, wenn wir entscheiden, dass für den Seitenbereich die Normale aus dem Körper heraus zeigen wird, dann muss für die oberen und unteren kreisförmigen Teile die Normale ebenfalls aus dem Körper heraus zeigen.

Inkonsistente Oberflächennormalen

Schließlich gibt es Flächen, die nicht an jedem Punkt eine Flächennormale mit konsistenten Ergebnissen aufweisen (z.B. das Möbiusband). Wird eine solche Fläche in Stücke zerlegt, auf jedem Stück eine Parametrisierung und entsprechende Flächennormale gewählt und die Stücke wieder zusammengesetzt, können die Normalenvektoren, die von verschiedenen Stücken stammen, nicht in Einklang gebracht werden. Das bedeutet, dass an irgendeiner Verbindungsstelle zwischen zwei Stücken Normalenvektoren in entgegengesetzte Richtungen zeigen. Eine solche Oberfläche wird als nicht orientierbar bezeichnet. Auf nicht orientierbaren Flächen können Vektorfelder nicht integriert werden.