Harmonische Reihe

In der Mathematik ist die harmonische Reihe die divergente unendliche Reihe:

∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}}=1+{\frac {1}{2}}}+{\frac {1}{3}}}+{\frac {1}{4}}}+{\frac {1}{5}}}+\cdots } $\sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

Divergent bedeutet, dass die Summe immer größer wird, je mehr Begriffe man hinzufügt. Sie geht nicht auf einen einzigen endlichen Wert zu.

Unendlich bedeutet, dass Sie jederzeit einen weiteren Begriff hinzufügen können. Es gibt keinen endgültigen Begriff in der Reihe.

Sein Name kommt von der Idee der Harmonik in der Musik: die Wellenlängen der Obertöne einer schwingenden Saite sind 1/2, 1/3, 1/4 usw. der Grundwellenlänge der Saite. Mit Ausnahme des ersten Begriffs ist jeder Begriff der Reihe das harmonische Mittel der Begriffe beider Seiten. Die Phrase harmonisches Mittel stammt ebenfalls aus der Musik.

Geschichte

Die Tatsache, dass die harmonische Reihe auseinanderklafft, wurde erstmals im 14. Jahrhundert von Nicole Oresme nachgewiesen, wurde aber vergessen. Beweise wurden im 17. Jahrhundert von Pietro Mengoli, Johann Bernoulli und Jacob Bernoulli erbracht.

Harmonische Sequenzen wurden von Architekten verwendet. In der Barockzeit verwendeten Architekten sie in den Proportionen von Grundrissen, Ansichten und in den Beziehungen zwischen architektonischen Details von Kirchen und Palästen.

Divergenz

Es gibt mehrere bekannte Beweise für die Divergenz der harmonischen Reihe. Einige von ihnen werden nachstehend aufgeführt.

Vergleichstest

Eine Möglichkeit, die Divergenz zu beweisen, besteht darin, die harmonische Reihe mit einer anderen divergenten Reihe zu vergleichen, wobei jeder Nenner durch die nächstgrößte Zweierpotenz ersetzt wird:

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\Anzeigestil {\beginnt {\ausgerichtet}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}}+{\frac {1}{5}}+{\frac {1}{6}}}+{\frac {1}{7}}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\farbig {rot}{\mathbf {4} {}+{\frac {1}{4}}+{\frac {1}{\farbig {rot}{\mathbf {8} {1}+{\frac {1}{\farbig {rot}{\mathbf {8} {1}+{\frac {1}{\farbig {rot}{\mathbf {8} {}+{\frac {1}{8}}+{\frac {1}{\farbig {rot}{\mathbf {16} {\cdots \end{aligned}} ${\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}}$

Jeder Term der harmonischen Reihe ist größer oder gleich dem entsprechenden Term der zweiten Reihe, und daher muss die Summe der harmonischen Reihe größer oder gleich der Summe der zweiten Reihe sein. Die Summe der zweiten Reihe ist jedoch unendlich:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\Anzeigestil {\begin{ausgerichtet}&{}1+\links({\frac {1}{2}}}\rechts)+\links({\frac {1}{4}}\!+\!{\frac {1}}Richtig)+\links({\frac {\an8}\}\!+\!{\frac {1}frac {8}\}\!+\!{\frac {1}{8}\}}rechts)+\links({\frac {1}{16}\}\!+\!{\ccdots \!+\!{\frac {1}{16}\right} +\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}}+{\frac {1}{2}}}+{\frac {1}{2}}}+\cdots =\infty \end{aligned}}} ${\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}$

Daraus folgt (durch den Vergleichstest), dass auch die Summe der harmonischen Reihen unendlich sein muss. Genauer gesagt beweist der obige Vergleich, dass

∑ n = 1 2 k 1 n ≥ 1 + k 2 {\displaystyle \sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}}} $\sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}$

für jede positive ganze Zahl $k$ .

Dieser Beweis, der von Nicole Oresme um 1350 vorgeschlagen wurde, gilt als ein Höhepunkt der mittelalterlichen Mathematik. Er ist auch heute noch ein Standardbeweis, der im Mathematikunterricht gelehrt wird.

Integraler Test

Es ist möglich, die Divergenz der harmonischen Reihe zu beweisen, indem man ihre Summe mit einem ungeeigneten Integral vergleicht. Betrachten Sie die in der Abbildung rechts dargestellte Anordnung der Rechtecke. Jedes Rechteck ist 1 Einheit breit und 1/n Einheit hoch, so dass die Gesamtfläche der unendlichen Anzahl von Rechtecken die Summe der harmonischen Reihe ist:

Fläche der Rechtecke = 1 + 1 2 + 1 3 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle {\begin{array}{c}{\text{\fläche}}\\\{\text{{\rechtecke}}\end{array}}=1+{\frac {1}{2}}}+{\frac {1}{3}}+{\frac {1}{4}}}+{\frac {1}{5}}+\cdots } ${\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

Die Gesamtfläche unter der Kurve $y =$ 1/x von 1 bis unendlich ist durch ein divergierendes unzulässiges Integral gegeben:

Fläche unter der Kurve = ∫ 1 ∞ 1 x d x = ∞ . {\Anzeigestil {\Beginn{Array}{c}{\Text{\Fläche unter}\\{\Text{Kurve}}\Ende{Array}}}=\int _{1}^{\einzigartig }{\frac {1}{x}}}\,dx=\einzigartig . } ${\begin{array}{c}{\text{area under}}\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .$

Da dieser Bereich vollständig in den Rechtecken enthalten ist, muss auch die Gesamtfläche der Rechtecke unendlich groß sein. Dies beweist, dass

∑ n = 1 k 1 n > ∫ 1 k + 1 1 x d x = ln ( k + 1 ) . {\darstellungsstil \sum _{n=1}^{k}{\frac {1}{n}}}>\int _{1}^{k+1}{\frac {1}{x}}}\,dx=\ln(k+1). } $\sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).$

Die Verallgemeinerung dieses Arguments wird als Integraltest bezeichnet.

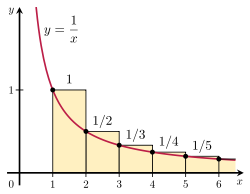
Illustration des Integraltests.

Rate der Divergenz

Die harmonische Reihe divergiert sehr langsam. Zum Beispiel ist die Summe der ersten ¹⁰⁴³ Terme weniger als 100. Das liegt daran, dass die Teilsummen der Reihe ein logarithmisches Wachstum aufweisen. Insbesondere

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1} $\sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1$

wobei $γ$ die Euler-Mascheroni-Konstante ist und $εk ~$ 1/2k, die sich 0 nähert, da $k$ unendlich wird. Leonhard Euler bewies sowohl dies als auch, dass die Summe, die nur die Kehrwerte der Primzahlen enthält, ebenfalls divergiert, d.h. auseinandergeht:

∑ p prime 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . {\displaystyle \sum _{p{\text{ prime }}}{\frac {1}{p}}}={\frac {1}{2}}+{\frac {1}{3}}}+{\frac {1}{5}}}+{\frac {1}{7}}+{\frac {1}{11}}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty . } $\sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .$

Teilbeträge

Die ersten dreißig harmonischen Zahlen
$n$	Teilsumme der harmonischen Reihe, $Hn$
$n$	ausgedrückt als Bruch		dezimal	relative Größe
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

Die endlichen Teilsummen der divergierenden harmonischen Reihen,

H n n = ∑ k = 1 n 1 k , {\darstellungsstil H_{n}=\summe _{k=1}^{n}{\frac {1}{k}},} $H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},$

werden harmonische Zahlen genannt.

Die Differenz zwischen $Hn$ und $ln n$ nähert sich der Euler-Mascheroni-Konstante an. Die Differenz zwischen zwei beliebigen harmonischen Zahlen ist niemals eine ganze Zahl. Keine harmonischen Zahlen sind ganze Zahlen, mit Ausnahme von $H1 = 1$ .

Verwandte Serien

Wechselnde harmonische Reihe

Die Reihe

∑ n = 1 ∞ ( - 1 ) n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{{n+1}}}{n}}}=1-{\frac {1}{2}}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots } $\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots$

ist bekannt als die alternierende harmonische Reihe. Diese Reihe konvergiert durch den Test der alternierenden Reihe. Insbesondere ist die Summe gleich dem natürlichen Logarithmus von 2:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2. {\Anzeigestil 1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}}+{\frac {1}{5}}-\cdots =\ln 2.} $1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.$

Die alternierende harmonische Reihe ist zwar bedingt konvergent, aber nicht absolut konvergent: Wenn die Terme in der Reihe systematisch neu geordnet werden, wird die Summe im Allgemeinen unterschiedlich und, abhängig von der Neuordnung, möglicherweise sogar unendlich.

Die Formel der alternierenden harmonischen Reihen ist ein Spezialfall der Mercator-Reihe, die Taylor-Reihe für den natürlichen Logarithmus.

Eine verwandte Reihe kann aus der Taylor-Reihe für den Arkustangens abgeleitet werden:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . {\darstellungsstil \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}}=1-{\frac {1}{3}}}+{\frac {1}{5}}}-{\frac {1}{7}}}+\cdots ={\frac {\pi }{4}}. } $\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.$

Dies ist als die Leibniz-Reihe bekannt.

Allgemeine harmonische Reihe

Die allgemeine harmonische Reihe hat die Form

∑ n = 0 ∞ 1 a n + b , {\darstellungsstil \sum _{n=0}^{\infty }{\frac {1}{an+b}},} $\sum _{n=0}^{\infty }{\frac {1}{an+b}},$

wobei $a \neq 0$ und $b$ reelle Zahlen sind, und b/a nicht Null oder eine negative ganze Zahl ist.

Durch den Grenzwertvergleichstest mit den harmonischen Reihen divergieren auch alle allgemeinen harmonischen Reihen.

$p-Reihe$

Eine Verallgemeinerung der harmonischen Reihe ist die $p-Reihe$ (oder hyperharmonische Reihe), definiert als

∑ n = 1 ∞ 1 n p {\darstellungsstil \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}} $\sum _{n=1}^{\infty }{\frac {1}{n^{p}}}$

für eine beliebige reelle Zahl $p$ . Wenn $p = 1 ist$ , ist die $p-Reihe$ die harmonische Reihe, die divergiert. Entweder der Integraltest oder der Cauchy-Kondensationstest zeigt, dass die $p-Reihe$ für alle $p > 1$ konvergiert $($ in diesem Fall nennt man sie die überharmonische Reihe) und für alle p divergiert $\leq 1.$ Wenn $p > 1$ , dann ist die Summe der p-Reihe ζ( $p), d.h.$ die Riemannsche Zeta-Funktion, die bei p ausgewertet wird.

Das Problem, die Summe für $p = 2 zu$ finden, wird das Baseler Problem genannt; Leonhard Euler zeigte, dass es sich um ^π2/6 handelt. Der Wert der Summe für $p = 3$ wird als Apéry-Konstante bezeichnet, da Roger Apéry bewiesen hat, dass es sich um eine irrationale Zahl handelt.

ln-Reihe

Mit der $p-Reihe$ verwandt ist die ln-Reihe, definiert als

∑ n = 2 ∞ 1 n ( ln n ) p {\darstellungsstil \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}} $\sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}$

für jede positive reelle Zahl $p$ . Dies kann durch den Integraltest gezeigt werden, der für $p \leq 1$ divergiert, aber für alle $p > 1$ konvergiert $.$

$φ-Reihe$

Für jede konvexe, reellwertige Funktion φ, so dass

lim sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , {\displaystyle \limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},} $\limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},$

die Reihe

∑ n = 1 ∞ φ ( 1 n ) {\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)} $\sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)$

ist konvergent. ^[]

Zufällige harmonische Reihe

Die zufällige harmonische Reihe

∑ n = 1 ∞ s n n , {\darstellungsstil \sum _{n=1}^{\infty }{\frac {s_{n}}{n}},} $\sum _{n=1}^{\infty }{\frac {s_{n}}{n}},$

wobei die $sn$ unabhängige, identisch verteilte Zufallsvariablen sind, die die Werte +1 und -1 mit gleicher Wahrscheinlichkeit 1/2 annehmen, ist ein bekanntes Beispiel in der Wahrscheinlichkeitstheorie für eine Reihe von Zufallsvariablen, die mit der Wahrscheinlichkeit 1 konvergiert. Die Tatsache dieser Konvergenz ist eine einfache Folge entweder des Kolmogorov-Drei-Serien-Satzes oder der eng verwandten Kolmogorov-Maximalungleichheit. Byron Schmuland von der University of Alberta untersuchte die Eigenschaften der harmonischen Zufallsreihen weiter und zeigte, dass die konvergente Reihe eine Zufallsvariable mit einigen interessanten Eigenschaften ist. Insbesondere nimmt die Wahrscheinlichkeitsdichtefunktion dieser Zufallsvariablen, die bei +2 oder bei -2 bewertet wird, den Wert 0,1249999999999999999999999999999999999999999999764... an, wobei sie sich von 1/8 um weniger als 10-42 unterscheidet. Schmulands Beitrag erklärt, warum diese Wahrscheinlichkeit so nahe bei, aber nicht genau bei 1/8 liegt. Der genaue Wert dieser Wahrscheinlichkeit ergibt sich aus dem unendlichen Kosinusproduktintegral $C2$ dividiert durch π.

Verarmte harmonische Reihen

Die verarmte harmonische Reihe, bei der alle Terme, in denen die Ziffer 9 irgendwo im Nenner vorkommt, entfernt sind, kann als konvergent dargestellt werden und ihr Wert ist kleiner als 80. Tatsächlich konvergiert die Reihe, wenn alle Terme, die eine bestimmte Ziffernfolge (in einer beliebigen Basis) enthalten, entfernt werden.

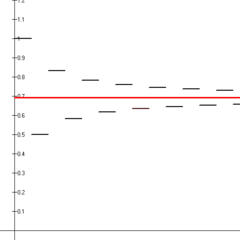
Die ersten vierzehn Teilsummen der alternierenden harmonischen Reihe (schwarze Liniensegmente) konvergieren zum natürlichen Logarithmus von 2 (rote Linie).

Bewerbungen

Die harmonische Reihe kann kontraintuitiv sein. Das liegt daran, dass es sich um eine divergierende Reihe handelt, auch wenn die Terme der Reihe kleiner werden und gegen Null gehen. Die Divergenz der harmonischen Reihe ist die Quelle einiger Paradoxa.

Der "Wurm auf dem Gummiband". Angenommen, ein Wurm krabbelt an einem unendlich elastischen Ein-Meter-Gummiband entlang, während das Gummiband gleichzeitig gleichmäßig gedehnt wird. Wenn sich der Wurm 1 Zentimeter pro Minute fortbewegt und sich das Band 1 Meter pro Minute dehnt, wird der Wurm dann jemals das Ende des Gummibandes erreichen? Die kontraintuitive Antwort lautet "ja", denn nach $n$ Minuten ist das Verhältnis zwischen der von der Schnecke zurückgelegten Strecke und der Gesamtlänge des Gummibandes

1 100 ∑ k = 1 n 1 k . {\Anzeigestil {\frac {1}{100}}\summe _{k=1}^{n}{\frac {1}{k}}}. } ${\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Da die Reihe beliebig groß wird, wenn $n$ größer wird, muss dieses Verhältnis schließlich über 1 liegen, was bedeutet, dass die Schnecke das Ende des Gummibandes erreicht. Der Wert von $n$ , bei dem dies geschieht, muss jedoch extrem groß sein: ungefähr e100, eine Zahl, die ¹⁰⁴³ Minuten (¹⁰³⁷ Jahre) überschreitet. Die harmonische Reihe divergiert zwar, aber nur sehr langsam.

Das Jeep-Problem fragt, wie viel Treibstoff ein Auto mit begrenzter Treibstoffkapazität insgesamt benötigt, um eine Wüste zu durchqueren und dabei Treibstofftropfen entlang der Route zurückzulassen. Die Strecke, die das Auto mit einer bestimmten Kraftstoffmenge zurücklegen kann, hängt von den Teilsummen der harmonischen Reihe ab, die logarithmisch wachsen. Der Treibstoffbedarf steigt also mit der gewünschten Distanz exponentiell an.

Das Problem des Blockstapelns: Bei einer Ansammlung von identischen Dominosteinen ist es möglich, sie an der Tischkante so zu stapeln, dass sie über die Tischkante hängen, ohne herunterzufallen. Das kontraintuitive Ergebnis ist, dass sie so gestapelt werden können, dass der Überhang so groß ist, wie man möchte. Das heißt, vorausgesetzt, es sind genügend Dominosteine vorhanden.

Ein Schwimmer, der jedes Mal schneller schwimmt, wenn er die Beckenwand berührt. Der Schwimmer beginnt ein 10-Meter-Becken mit einer Geschwindigkeit von 2 m/s zu durchqueren, und bei jeder Überquerung werden der Geschwindigkeit weitere 2 m/s hinzugefügt. Theoretisch ist die Geschwindigkeit des Schwimmers unbegrenzt, aber die Anzahl der Beckenüberquerungen, die erforderlich sind, um diese Geschwindigkeit zu erreichen, wird sehr groß; um beispielsweise die Lichtgeschwindigkeit zu erreichen (ohne Berücksichtigung der speziellen Relativitätstheorie), muss der Schwimmer das Becken 150 Millionen Mal überqueren. Im Gegensatz zu dieser großen Zahl hängt die Zeit, die benötigt wird, um eine bestimmte Geschwindigkeit zu erreichen, von der Summe der Serien bei einer bestimmten Anzahl von Beckenkreuzungen ab:

10 2 ∑ k = 1 n 1 k . {\darstellungsstil {\frac {10}{2}}\summe _{k=1}^{n}{\frac {1}{k}}}. } ${\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Die Berechnung der Summe zeigt, dass die Zeit, die benötigt wird, um zur Lichtgeschwindigkeit zu gelangen, nur 97 Sekunden beträgt.

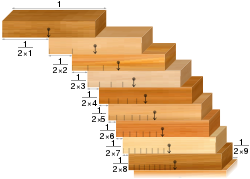
Das Block-Stapel-Problem: Blöcke, die entsprechend der harmonischen Reihe ausgerichtet sind, überbrücken Spaltungen beliebiger Breite.

Fragen und Antworten

F: Was ist die harmonische Reihe?

A: Die harmonische Reihe ist eine unendliche divergente Reihe, bei der jeder Term gleich 1 geteilt durch seine Position in der Reihe ist.

F: Was bedeutet es, dass eine Reihe divergent ist?

A: Divergent bedeutet, dass die Summe beim Hinzufügen weiterer Terme immer größer wird und nicht auf einen einzigen endlichen Wert zusteuert.

F: Was bedeutet es, wenn eine Reihe unendlich ist?

A: Unendlich bedeutet, dass Sie immer einen weiteren Term hinzufügen können und es keinen letzten Term in der Serie gibt.

F: Woher stammt der Name dieser Serie?

A: Der Name dieser Reihe stammt von der Idee der Obertöne in der Musik, bei der die Wellenlängen der Obertöne 1/2, 1/3, 1/4 usw. der Grundwellenlänge der Saite betragen.

F: Was ist ein harmonischer Mittelwert?

A: Von einem harmonischen Mittelwert spricht man, wenn jeder Term in einer Folge gleich dem harmonischen Mittelwert seiner benachbarten Terme ist. Auch dieser Ausdruck stammt aus der Musik.

F: Wie berechnen wir die einzelnen Terme in dieser Sequenz?

A: Jeder Term in dieser Sequenz kann berechnet werden, indem man eins durch seine Position in der Sequenz (1/n) dividiert.